Koordinatentransformation

Die Umrechnung von Koordinaten eines Punktes in ein anderes Koordinatensystem bezeichnet man als Koordinatentransformation.

Unterschiedliche geodätische Koordinatensysteme sind im Allgemeinen unterschiedlich im Erdkörper gelagert. Zur Transformation zwischen diesen Systemen muss daher die gegenseitige Lage der beiden betroffenen Systeme bekannt sein. Um die Parameter einer Transformationsvorschrift bestimmen zu können, benötigt man je nach Transformationsansatz eine gewisse Anzahl von Identpunkten, das sind Punkte mit bekannten Koordinaten in beiden Systemen.

Die folgenden drei Transformationsmodelle sind im BEV-Transformator implementiert:

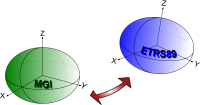Die 7-Parameter-Transformation ist eine konforme (winkeltreue) Transformation, bei der der Systemübergang mit einer Verschiebung des Koordinatenursprungs, einer Verdrehung der beiden Systeme und einem Maßstabsfaktor modelliert wird. Der Maßstabsunterschied beider Systeme resultiert vor allem aus der unterschiedlichen Genauigkeit in der Realisierung.

• Verschiebungsvektor $\vec{\Delta X}$
• Drehungen $r_x$, $r_y$ und $r_z$
• Maßstabsfaktor m

$\vec{X_{neu}} = \vec{ \Delta X } + \left(1+m\right) \cdot R \cdot \vec{ X_{alt} }$

mit der Rotationsmatrix

$$R = \begin{pmatrix} 1 & 0 & 0\\\\ 0 & cos(r_x) & sin(r_x)\\\\ 0 & -sin(r_x) & cos(r_x) \end{pmatrix} \begin{pmatrix} cos(r_y) & 0 & -sin(r_y)\\\\ 0 & 1 & 0\\\\ sin(r_y) & 0 & cos(r_y) \end{pmatrix} \begin{pmatrix} cos(r_z) & sin(r_z) & 0\\\\ -sin(r_z) & cos(r_z) & 0\\\\ 0 & 0 & 1 \end{pmatrix}$$

oder für sehr kleine Winkel

$$ R = \begin{pmatrix} 1 & r_z & -r_y \\\\ -r_z & 1 & r_x \\\\ r_y & -r_x & 1 \end{pmatrix} $$

Die Schreibweise der Rotationsmatrix wird als _Coordinate-Frame Model_ bezeichnet. Die Drehungen beschreiben die Rotation der Koordinatenachsen, und nicht die Rotation des Position-Vektors _(Position Vector Model)_.

Dies entspricht auch der Schreibweise der vom BEV abgegebenen Transformationsparameter.

beschreibt eine Ähnlichkeitstransformation in der Ebene. Eine Ähnlichkeitstransformation ist eine winkeltreue Transformation, welche eine Verschiebung und Verdrehung des Ausgangskoordinatensystems vorsieht. Um unterschiedliche Genauigkeiten in der Realisierung der betroffenen Koordinatensysteme zu berücksichtigen, bringt man zusätzlich einen Maßstabsfaktor m an. Die Änderung von Strecken und Flächen ist von der Größe dieses Maßstabfaktors abhängig.

- Verschiebungsvektor $\vec{ \Delta X}$ - Drehung $\alpha$ - Maßstabsfaktor m

$\vec{X_{P}} = \vec{\Delta X} + mR\vec{X_{P}^{'}}$

mit der Rotationsmatrix

$$ R = \begin{pmatrix} cos(\alpha) & sin(\alpha) \\\\ -sin(\alpha) & cos(\alpha) \end{pmatrix} $$

$$ \begin{pmatrix} y_{P} \\\\ x_{P} \end{pmatrix} = \begin{pmatrix} y_{0} \\\\ x_{0} \end{pmatrix} + m\begin{pmatrix} cos\alpha & sin\alpha \\\\ -sin\alpha & cos\alpha \end{pmatrix}\begin{pmatrix} y_{P}^{'} \\\\ x_{P}^{'} \end{pmatrix} $$

Eine Transformationsfläche bildet ein regelmäßiges Raster über ein bestimmtes Gebiet, z.B. das österreichische Staatsgebiet. Die Datumstransformation zwischen MGI und ETRS89 erfolgt dabei durch Interpolation von Verschiebungswerten aus den „Shifts“ der Rasterpunkte. Ein großer Vorteil dieser Methode liegt darin, dass für den gesamten Definitionsbereich der Transformationsfläche ein stetiger Transformationsverlauf gegeben ist. Somit ergeben sich bei der Transformation benachbarter Gebiete keine Unstetigkeitsstellen im Übergangsbereich. Das regelmäßige Raster für die flächenbasierte Transformation wird in der Regel aus einer Vielzahl von Identpunkten abgeleitet. Dazu werden ebenfalls Interpolationsverfahren angewendet. Der Abstand der Rasterpunkte bestimmt dabei die Genauigkeit, mit der eine Transformation zwischen den beiden Systemen durchgeführt werden kann. Ein sinnvoller Abstand zwischen den Rasterpunkten wird durch die Dichte der Identpunkte bestimmt, aus dem dieser Raster abgeleitet wird.

Das GIS-Grid ist eine vom BEV im Jahr 2010 entwickelte Transformationsfläche für den Datumsübergang zwischen dem Europäischen Bezugssystem ETRS89 und dem System der österreichischen Landesvermessung MGI. Es wurde aus 28.120 Triangulierungspunkten 1. - 5. Ordnung abgeleitet, für die neben den Landeskoordinaten auch Koordinaten im ETRS89 vorlagen. Punkte mit aus Mehrfachmessungen nachgewiesenen Bodenbewegungen wurden von der Modellbildung ausgenommen. Aus diesen Modellpunkten wurde mit dem Kriging-Interpolationsverfahren ein regelmäßiges Raster im System MGI generiert, wobei die Rasterweite 30„ in Länge und 45“ in Breite beträgt. Dies entspricht einem Punktabstand von etwa 1000m in Ost-West und auch in Nord-Süd.

Jedem dieser Stützpunkte ist jeweils ein Verschiebungswert dφ und dλ zugewiesen, welche zur Umrechnung zwischen den Ellipsoiden GRS80 und Bessel an die ellipsoidischen Koordinaten φ und λ anzubringen sind. Durch Interpolation der Shiftwerte dφ und dλ für einen beliebigen Punkt kann dieser in das jeweils andere Datum übergeführt werden.

Bei Verwendung dieser Transformationsfläche ist eine österreichweite Lagetransformation mit einer absoluten Genauigkeit von kleiner als 15cm möglich, wobei die Transformation zwischen den beiden Systemen ETRS89 und MGI bidirektional anwendbar ist.

Das GIS-Grid ist im BEV-Transformator (Austrian Mode) integriert und wird vom BEV auch in Form von zwei Produkten angeboten:

• NTv2-Datei für GIS-Anwendungen
• Korrekturwerte bei Nutzung des APOS-Echtzeitpositionierungssystems